Orbital Mechanics
Orbital mechanics or astrodynamics is the application of celestial mechanics to the practical problems concerning the motion of rockets and other spacecraft.
- Early Space Exploration
- Kepler's Laws
- Gravity
- Orbit Around the Earth
- Low Earth Orbit
- How to Describe an Orbit
- Defining the Classical Orbital Elements
- Satellite Ground Tracks
- Field of View
Early Space Exploration
- Nicolaus Copernicus (1473-1543)
- Placed Sun at center of solar system
- Showed Earth rotates on its axis once a day
- Thought planets orbit in uniform circles (wrong!)
- Johannes Kepler (1571-1630)
- Discovered orbit of Mars was not circular
- Concluded that planets move around the Sun in elliptical orbits with the Sun not at the center but at a focus
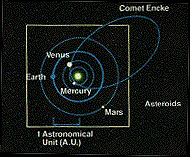
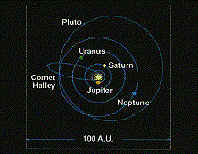
Kepler's Laws
- Kepler's 1st Law:
- The orbits of the planets are ellipses with the Sun at one focus.

- Kepler's 2nd Law:
- The line joining a planet to the Sun sweeps out equal area in equal times.
* This means that the closer a planet is to the Sun, the faster it will travel.
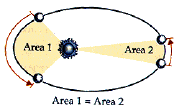
- The line joining a planet to the Sun sweeps out equal area in equal times.
- Kepler's 3rd Law:
- The square of an orbital period is directly proportional to the cube of the average distance between the Sun and a planet:

* This means that the farther a planet is from the Sun, the longer it takes to go around.
* If you know the distance of a planet from the Sun, you know how long that planet takes to go around.

- The square of an orbital period is directly proportional to the cube of the average distance between the Sun and a planet:
Gravity
Gravity is the idea that two (or more) chunks of matter tend to attract to each other. The more mass they have, the more they will attract.
- Galileo Galilei (1564-1642)
- Used telescopes to revolutionize our understanding of the Universe
- Discovered that all objects regardless of mass fall at the same rate when dropped from the same height (if air resistance is neglected).
- Isaac Newton (1642-1727)
- Worked out laws of motion and gravity, revolutionizing our understanding of the world.
- Orbits of planets and satellites are based on Newton's laws!
- Newton's Laws:
- A body at rest or moving in a straight line at a constant speed stays that way unless a force is applied to it.
- A body's mass times its acceleration is equal to the applied force (F=Ma).
- To every action there is always opposed an equal reaction.
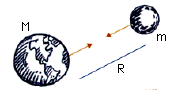
- Newton's Universal Law of Gravitation:
- The force of gravity between two bodies is directly proportional to the product of their masses and inversely proportional to the square of the distance between them.

Orbit Around the Earth
- Orbit
- An orbit is a fixed path in space that a spacecraft follows. Depending on the mission, the size, shape, and orientation of an orbit will vary.
- Satellite
- A satellite is any object in orbital motion (for example, the Sun, Moon, Earth, a spacecraft, or the space shuttle).
- The laws that determine the orbital motion of a satellite are the same, no matter what larger body the satellite orbits.
- The Earth's gravity determines the size and shape of the orbit of a nearby spacecraft.
- The law of gravity requires that the spacecraft must orbit in a plane that passes through the center of the Earth.

- All Earth-orbiting satellites must orbit in space to avoid collisions with the trillions of air molecules from the atmosphere that surround the surface of the Earth.
- Space begins at about 100 miles above the surface of the Earth, where the air is so thin that it has little effect on a spacecraft.
- A satellite is any object in orbital motion (for example, the Sun, Moon, Earth, a spacecraft, or the space shuttle).
Low Earth Orbit
Low Earth Orbit (LEO) is a type of orbit. The space shuttle flies in a Low Earth Orbit. The altitude in LEO varies from 100 to 300 miles above the Earth's surface. (Communication satellites orbit at approximately 25,000 miles from Earth.) Since it takes the shuttle about 90 minutes to complete one orbit around the globe, it can complete 16 to 17 orbits in one day. On a relative scale, the shuttle orbits the Earth very close to its surface.
NOTE: An object in Low Earth Orbit is in an elliptical orbit. (A circular orbit is simply a special case of an elliptical orbit.)

NOTE: An object in Low Earth Orbit is in an elliptical orbit. (A circular orbit is simply a special case of an elliptical orbit.)
How to Describe an Orbit
There are six Classical Orbital Elements (see next section) that are necessary for us to know about an orbit and a satellite's place in it. These elements help us describe:
- Orbit size
- Orbit shape
- Orbit orientation
- Orbit location
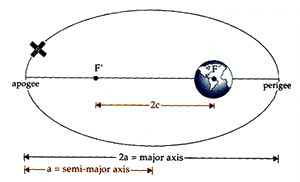
Elliptical Geometry

- An ellipse looks like an oval, or squashed circle.
- The longest line drawn from one end of the ellipse (through the center) to the other side is called the major axis (2a).
- Every ellipse has two foci (F and F'), and the distances between each focus and the center of the ellipse are equal (c). In a circle, the two foci lie on top of each other.
- The point on the semi-major axis closest to the Earth is called the perigee, while the point on this axis farthest from the Earth is called the apogee.
Defining the Classical Orbital Elements
- Semi-major Axis
- The size of the orbit is described by the semi-major axis (a), which is one-half the distance across the major (long) axis of the orbit.
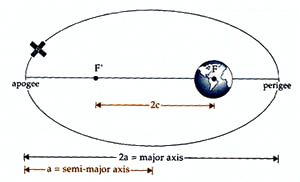
- The size of the orbit is described by the semi-major axis (a), which is one-half the distance across the major (long) axis of the orbit.
- Eccentricity
- Eccentricity (e) specifies the shape of an orbit and is given by the ratio of the distance between the two foci and the length of the major axis.
e = 2c/2a
The eccentricity of a circular orbit is zero, and can range from zero to less than one for an ellipse.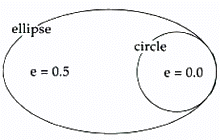
- Eccentricity (e) specifies the shape of an orbit and is given by the ratio of the distance between the two foci and the length of the major axis.
- Inclination (i) [degrees]
- The angle between the plane of the equator and the orbital plane.
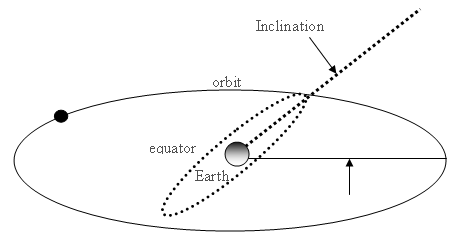
- The angle between the plane of the equator and the orbital plane.
- Right Ascension of the Ascending Node (Ω)
- The angle between the Sun and the intersection of the equatorial plane and the orbit on the first day of spring in the Northern Hemisphere. The day is called the vernal equinox. Looking down from above the North Pole, the right ascension of the ascending node is positive counter-clockwise.
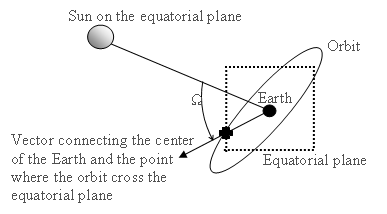
- The angle between the Sun and the intersection of the equatorial plane and the orbit on the first day of spring in the Northern Hemisphere. The day is called the vernal equinox. Looking down from above the North Pole, the right ascension of the ascending node is positive counter-clockwise.
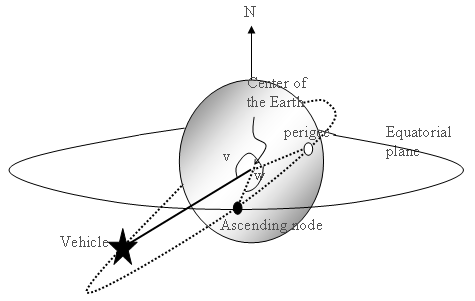
- Argument of Perigee (w) [degrees]
- The angle between the ascending node and the orbit's point of closest approach to the Earth (perigee).
- True Anomaly (v)[degrees]
- The angle between the perigee and the vehicle in the orbit plane.
Satellite Ground Tracks
The Six Classical Orbital Elements allow us to describe what an orbit looks like in space. What we need to know next is what part of the Earth the satellite is passing over at any given time. A groundtrack shows the location on the Earth that the spacecraft flies directly over during its orbital path around the Earth. To understand groundtracks, we need to know the following:
The groundtrack follows what is called a great circle route around the Earth. A great circle is any circle which cuts through the center of the Earth. All groundtrack drawings use the latitude/longitude system.
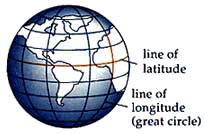
Latitude: Latitude measures how far north or south a point lies off the equator. The equator is at zero degrees latitude, the North Pole is at 90 degrees north latitude and the South Pole is at 90 degrees South latitude.
Longitude: Longitude measures how far east or west a point lies from an imaginary line that runs from the North Pole to the South Pole through Greenwich, England. This line is called the Prime Meridian. The longitude varies from 0 degrees at the prime meridian to 180 degrees west and 180 east.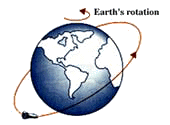
How does this affect the groundtracks? Even though the spacecraft orbit stays fixed in space, the Earth rotates to the east. So to a point fixed on the Earth, the spacecraft appears to shift to the west during successive orbits.
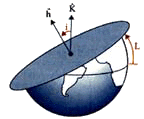
The highest latitude reached by a satellite orbit is equal to its inclination.
To illustrate this concept, the following groundtracks represent orbits with the same period, but A has an inclination of 10 degrees, B has an inclination of 30 degrees, C has an inclination of 50 degrees, and D has an inclination of 85 degrees.

The groundtrack follows what is called a great circle route around the Earth. A great circle is any circle which cuts through the center of the Earth. All groundtrack drawings use the latitude/longitude system.

Latitude: Latitude measures how far north or south a point lies off the equator. The equator is at zero degrees latitude, the North Pole is at 90 degrees north latitude and the South Pole is at 90 degrees South latitude.
Longitude: Longitude measures how far east or west a point lies from an imaginary line that runs from the North Pole to the South Pole through Greenwich, England. This line is called the Prime Meridian. The longitude varies from 0 degrees at the prime meridian to 180 degrees west and 180 east.
- Groundtrack drawings appear on a Mercator projection of the Earth's surface. This type of map allows the entire surface of the round world to appear on a rectangle.
- The projection of a spacecraft orbit on a flat map (Mercator projection) looks like a sine wave. This is the spacecraft's groundtrack.
- If the Earth did not rotate, the groundtrack of an orbit would continuously repeat. But, the Earth spins eastward on its axis at nearly 1,000 mph at the equator while the spacecraft orbits around it.

How does this affect the groundtracks? Even though the spacecraft orbit stays fixed in space, the Earth rotates to the east. So to a point fixed on the Earth, the spacecraft appears to shift to the west during successive orbits.

The highest latitude reached by a satellite orbit is equal to its inclination.
To illustrate this concept, the following groundtracks represent orbits with the same period, but A has an inclination of 10 degrees, B has an inclination of 30 degrees, C has an inclination of 50 degrees, and D has an inclination of 85 degrees.

Field of View
Field of View (FOV) is the angle that describes the amount of the Earth's surface the spacecraft can see at any given time.
The higher the spacecraft is above the Earth, the more you can see. Thus, the size of the orbit determines the spacecraft's field of view. The area of coverage on the Earth's surface is called the swath width.

The higher the spacecraft is above the Earth, the more you can see. Thus, the size of the orbit determines the spacecraft's field of view. The area of coverage on the Earth's surface is called the swath width.

Test Yourself
To see how much you have learned, test yourself with the Orbital Mechanics Quiz!| Take the Orbital Mechanics Quiz |







